@adlrocha - From Turing to Shannon
On the importance of theoretical computer science.
What does it mean to be a good theoretical computer scientist? What path should one follow to become one? It suffices to earn a computer science degree, or would it be best to study a maths or a physics degree and then join the field of computer science? When it was my turn to make this decision I didn’t know the meaning of computer science (more so since in Spain we don’t have a proper computer science degree). Even less what a theoretical computer scientists did for a living. I just happened to like programming, computers and telecommunications. And that’s how I ended up in the practical side of this spectrum earning my telecommunications and electrical engineering degrees.
What I didn’t know then and that I’ve realized after years of reading quite a few books on cryptography, computational complexity, and information theory (including the quantum cousins of these fields) is: how exciting theoretical fields can be; how important they are to foster practical advancements; and how much I miss not having studied a math or physics degree before telecommunications or computer science to equip myself with the theoretical skills required to do groundbreaking research.
If you asked me now the question of “what path should one follow to become a good telecommunication or computer science researcher?” My answer would be, if you want to be involved in “fundamental research”, study a physics or maths degree. You will always have time to switch to the practical side of the force, and learn what is needed to be a good engineer. Build your mathematical mindset, and then create your “engineering sixth sense”.
Of course, this quite a biased opinion fruit of my experience, but to support my claim I will share the story of two mathematicians that became the fathers of computation and information theory, respectively: Turing and Shannon.
Turing’s Machines and Halting Problem
Alan Turing was an English mathematician highly influential in the development of theoretical computer science. His name appears all over computer science: in concepts such as Turing complete programming languages, Turing machines, or the Turing test. But all of these ideas are the result of the the resolution of a mathematical problem: the Entscheidungsproblem, that can be summarized in the following question “is mathematics decidable?” Which declines into, “is there a definite procedure to show if a mathematical statement is true or false?”. Turing managed to solve this problem showing the undecidability of mathematics through his “halting problem”.
To prove the “halting problem”, and thus undecidability of the Entscheidungsproblem, he first needed to formally describe what a definite procedure was. To do so he invented an widely known apparatus, the Turing machine. A Turing machine is a mathematical model of computation that defines an abstract machine, which manipulates symbols on a strip of tape according to a table of rules. The machine operates on an infinite memory tape divided into discrete "cells". The machine positions its "head" over a cell and "reads" or "scans" the symbol there. Then, as per the symbol and the machine's own present state in a "finite table" of user-specified instructions, the machine (i) writes a symbol (e.g., a digit or a letter from a finite alphabet) in the cell (some models allow symbol erasure or no writing), then (ii) either moves the tape one cell left or right (some models allow no motion, some models move the head), then (iii) (as determined by the observed symbol and the machine's own state in the table) either proceeds to a subsequent instruction or halts the computation.
A Turing machine is capable of simulating any algorithm's logic, so it was the perfect construction to formalize a definite procedure. With definite procedures fomrmally defined, if he was able to program any mathematical proof into a Turing machine, it would mean that mathematics is decidable, as there would be a definite procedure to solve any possible proof in maths. Unfortunately, this isn’t the case, and to prove so he came up with his “halting problem”.
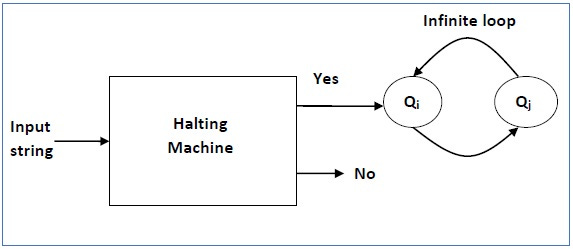
The Halting Problem can be described as the problem of finding whether, for a given input, a program will halt at some time or continue to run indefinitely. To prove it, Turing first assumed that such a Turing machine exists to solve this problem, to then show this can be it, as it is contradicting itself. We will call this Turing machine that is able to identify if programs halts or not a Halting machine that produces a “yes” or “no” in a finite amount of time. If the halting machine finishes in a finite amount of time, the output comes as “yes”, otherwise as “no”. The following is the block diagram of a Halting machine:
We are considering that the halting machine is decideable, so we can design its complementary machine, an inverted halting machine (HM)’ which can be described as: if H returns YES, then loop forever, if H returns NO, then halt. The following is the block diagram of an “Inverted halting machine”:
Now, let design a halting machine (HM)2 which inputs its own as the input to the machine. If we assume that the halting machine exist, then the inverted halting machine must exist, what gets us to a contradiction in (HM)2. Hence, the halting problem is undecidable.
I may have lost many of you by now, so let’s use some visual aide to help you understand this impressive proof:
In order to solve this proof, Turing had to invent the Turing machine, a model that would set the groundwork for modern computers. With this mental model Turing invented a programmable computer before the first practical one was even the built. This our first great example of how answering a fundamental theoretical questions can lead to impressive practical advancements.
Shannon, the father of information theory
We’ve already talked about this guy in this newsletter. Shannon was a mathematician, electrical engineer, cryptographer and, more importantly, the father of information theory. His "A Mathematical Theory of Communication" paper from 1948 set the foundation for all the revolution yet to come in telecommunications. Again, this paper is highly theoretical work that focuses on the problem of how best to encode all the information a sender wants to transmit. Shannon developed information entropy as a measure of the information content in a message, which is a measure of uncertainty reduced by the message. Something that still impresses me about Shannon’s work is how he gets inspiration from a physical concept, the thermodynamical entropy, to describe such an abstract concept as the amount of information inamessage.
Shannon’s outstanding theoretical set the foundation to many impressive practical applications in the fields of mobile communications, natural language processing, sampling theory, computational linguistics, etc. Have you heard of the Shannon theorem or the Shannon-Hartley theorem? These theorems tell the maximum rate at which information can be transmitted over a communications channel and a channel of a specified bandwidth in the presence of noise, respectively. Something every electrical engineering and telecommunications engineering student has studied in his bachelor’s (so as you may have guessed, this guy kind of like a hero to me).
Another impressive fundamental result from a theorist that managed to change the future of many practical fields.
Maths, theoretical computer science, information theory and physics are all connected
Like these, many other theoretical results have been key for new practical developments in computer science, information theory and physics. From recent developments in artificial intelligence, to new constructions in cryptography (with brand zero-knowledge proofs and multiparty computation primitives), and theoretical bounds in physics.
A recent example of the importance of theoretical computer science is this paper that shows how “the class MIP* of languages that can be decided by a classical verifier interacting with multiple all-powerful quantum provers sharing entanglement is equal to the class RE of recursively enumerable languages”. This paper can potentially have a significant impact in disjoint fields such as computer science, physics and maths (just like it happened with Turing and Shannon’s work). This post gives a good overview of the potential impact of this publication may have.
With quantum information and quantum computation gaining traction and becoming increasingly important, I feel we are approaching a new golden age of theoretical computer science. So if you asked me again what can you do to become a great theoretical computer scientist and to contribute to fundamental research I would answer “first get some math and physics skills, and then jump to computer science. This will give you the skills to make better sense of the abstract computer science world”.
I would love to hear your take on this. Any thoughts? If not, see you next week!